The Five Proficiencies
On April 30th, 2019, the draft curriculum for Wales was published on HWB. The curriculum is organised into six Areas of Learning and Experience, and I am proud to be part of the team of teachers developing the Mathematics and Numeracy AOLE.
Initial work involved background reading and research, including researching other countries’ curricula. Similar to the path taken by Lucy Crehan in her excellent book Cleverlands, we browsed the curricula from such countries as Finland, Singapore and Canada, finding that the organising frameworks for each curriculum were similar, based (broadly) upon Number, Algebra, Geometry and Statistics. It is no surprise, therefore, that the new Welsh curriculum is based upon these headings, thus forming the “What Matters” statements for Mathematics and Numeracy.
What has changed in the new curriculum is the shift in emphasis from the “What” (the content of the curriculum) to the “What and How”. The new curriculum contains reference to five new mathematical proficiencies, which talk about how to teach mathematics and numeracy.
- Conceptual understanding: Mathematical concepts and ideas should be dwelt on, built on, and connected together as learners experience increasingly complex mathematical ideas. Learners demonstrate conceptual understanding by explaining and expressing concepts, finding examples (or non-examples) and by representing a concept in a variety of ways, including verbal, concrete, visual, digital and abstract representations.
- Communication with symbols: Learners should understand that the symbols they are using are abstract representations and should develop greater flexibility in their application and manipulation of an increasing range of symbols, understanding the conventions of the symbols they are using.
- Strategic competence: (i.e. formulating problems mathematically in order to solve them) Learners should become increasingly independent in recognising and applying the underlying mathematical structures and ideas within a problem, in order to be able to solve them.
- Logical reasoning: As learners experience increasingly complex concepts, they should also develop an understanding of the relationships between and within these concepts. They should apply logical reasoning about these relationships and be able to justify and prove them. Justifications and proof should become increasingly abstract, moving from verbal, visual or concrete explanations to representations involving symbols and conventions.
- Fluency: As learners experience, understand and apply increasingly complex concepts and relationships, fluency in remembering facts, relationships and techniques should grow. As a result, facts, relationships and techniques learned previously should become firmly established, memorable and usable.
It was clear that an increased focus on pedagogy was needed. The first recommendation of the 2015 Mathematics Task and Finish report stated that
- “In collaboration with consortia and local authorities, school leaders and governors should evaluate current practice at school and consortium level as to what excellent mathematics teaching and learning looks like”.
A 2014 interim Estyn report stated that
- “Pupils’ numerical reasoning skills are still not strong enough.”
- “Only around half of schools have developed suitable provision for numeracy.”
- “In most primary and secondary schools, planning and provision for numeracy are weaker than for literacy.”
- “In general, the quality of marking pupils’ numeracy work across the curriculum is not good enough.”
Our development of the proficiencies started with looking at a major American report, Adding It Up, edited by Jeremy Kilpatrick et al. Page 5 of the Executive Summary contains the following picture summarising “five intertwined strands of proficiency”.

This picture shows clearly that even though mathematical proficiencies can be listed individually, they are highly inter-related.
Other curricula have already incorporated mathematical proficiencies. For example, the Australian mathematics curriculum is based around the four proficiencies of “understanding, fluency, problem-solving and reasoning”. For Wales, the group worked with Anne Watson, Emeritus Professor of Mathematics Education at the University of Oxford, in developing the five proficiencies listed above. But what do they mean in practice? To explore this, let us consider planning a series of lessons on the area of two-dimensional shapes.
The Area of Two-Dimensional Shapes
Conceptual Understanding
Asked the question “What is the area of a rectangle?”, the vast majority of GCSE pupils will respond with a variation of “length multiplied by width”. This shows not conceptual understanding, but a fluency in remembering a formula associated with the area of a rectangle. The concept of the area of a rectangle is the amount of space the rectangle takes up in two dimensions, within the boundary of the four straight edges of the rectangle. This is the real answer to “what is the area of a rectangle?”, but how can we develop this understanding in learners? We could attempt to introduce this definition, and have learners try to remember it, but in my opinion, this would be the wrong path. Learners need to experience mathematics, and the best way to learn mathematics is to do mathematics. Task design is crucial here. Here is a task, designed by John Mason and discussed on this episode of the Mr. Barton Maths Podcast, that could lead to better conceptual understanding.
The task involves drawing shapes on the grid that satisfy the stated conditions. For example, the shape in the top left should have a perimeter less than the perimeter of the purple shape in the middle, and an area that is more than the area of the purple shape in the middle. When completing this task, you will find yourself thinking hard about the concepts of perimeter and area, and not just blindly following a formula.
Communication with Symbols
This proficiency is one that is unique to Wales, and can be illustrated here by considering the following question: calculate the perimeter and area of the following triangle.

Here is a selection of my students’ responses to this question.



In the first response, the answers are correct, but the student has not communicated their method of finding the answers. This could potentially lose a method mark in a GCSE examination.
In the second response, there is a numerical error in calculating the area, but there is also an incorrect use of the equals sign. The expression at the start of the line, 6 × 4.5, is equal to 27, but this is not equal to what follows: the expression after the first equals sign is 27 ÷ 2, which is equal to 13.5, not 27. This error is commonly seen, and is often left uncorrected in students’ books. Communication with symbols is about understanding the conventions of mathematical symbols, and includes the correct use of the equals sign.
The third response sets out the area calculation correctly, but fails to include a unit for the perimeter answer – another common error.
Strategic Competence
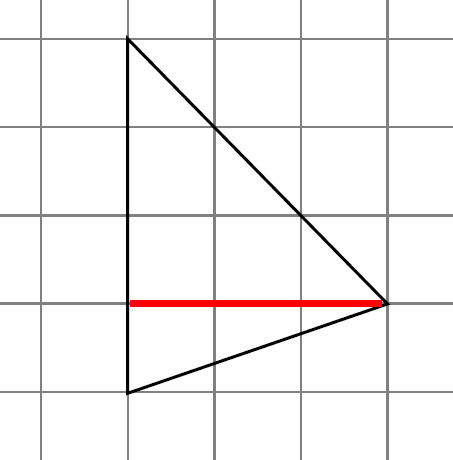
To me, strategic competence is about possessing a bank of strategies, a mathematical toolbox if you like, for tackling different mathematical situations. In the context of area, a student would need a strategy for finding the area of the following triangle.

One strategy may be to take the edge of length 4 units as the base of the triangle, note that the triangle then has height 3 units, and use the formula for the area of the triangle to calculate the answer. Another strategy may be to split the triangle into two smaller triangles, as shown below, and calculate the area of the two smaller triangles – perhaps using the rectangles surrounding the smaller triangles?
To develop strategic competence, students should be exposed
to different methods and problem solving strategies – Third Space Learning’s free
guide to problem solving techniques is a good starting point.
Logical Reasoning
In a Welsh context, “reasoning” has for some years now been linked to the national numeracy tests, which have a reasoning part each year. For example, here is a question from the year 8 sample assessment materials.

The logical reasoning proficiency includes being able to answer such questions from the national reasoning tests, but it also encompasses much more. Note the reference to “justify” and “prove” in the description of the proficiency. In the context of area, we could explore why the area of a parallelogram is base × height…

…or we could explore the formula giving the area of a trapezium.

Fluency
Finally, we come to the fluency proficiency. To become fluent in using a technique, students should still be expected to complete a set of exercises on, say, finding the area of a rectangle – this mode of working will not disappear from classrooms.

The key is that the above exercise should not be the only
thing that students complete on finding the area of a rectangle – each proficiency
must be considered during the planning stage. This is not to say that all
proficiencies should appear in every topic – they should not be viewed
as a tick list – rather they should form the basis for what activities should be
completed to understand, in depth, a particular topic.
Dr. Gareth Evans
June 2019
P.S. Here is a video of mine showing how to consider the proficiencies when planning a sequence of lessons on solving linear equations. (This video was shown during the recent mathematics and numeracy engagement events across Wales.)
